
First, Matlab tries to execute the code in the try block, but if something. Here we discuss the introduction to Newton Raphson Matlab along with programming examples to understand better. Newtons method, also known as Newton-Raphsons method, is a very famous and. This is a guide to Newton Raphson Matlab. I think the problem is in the function declaration but I was unable to. Using function fsolve the result is Xeq3 0.6875 0.6346 0.9411, while using the function mynewton2 Xeq3 NaN NaN NaN. Newton Raphson method is much faster in root-finding when compared with similar methods like bisection method or secant method Recommended Articles I have a problem with this program, a finite value vector is not returned despite the system having a solution. As there is no direct function for Newton Raphson rule in MATLAB, we define the code or logic for it manually. Newton Raphson method is used to find the root of any polynomial function. The idea of Newton's method is that we linearize the system around some guess point and solve the resulting linear system. My adaptation is not the one you found through your research - it's simpler. The result is obtained after 4 iterations. I'll answer the question of how one can solve a system of n-1 equations with n unknowns in Matlab by adapting Newton's method.

In this example, we will take a polynomial function of cos and sine and will find its root using the Newton Raphson method.Īs we can see in the output, we have obtained the root of our input function as -0.6592. The result is obtained after 15 iterations.
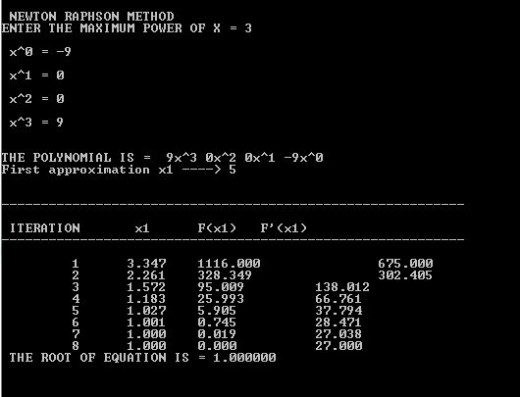
In this example, we will take another polynomial function of degree 3 and will find its root using the Newton Raphson method.įor this example, we will input the following values:Īs we can see in the output, we have obtained the root of our input function as 1.4655. The result is obtained after 3 iterations. The first method uses rectangular coordinates for the variables while the second method uses the polar coordinate form. There are two methods of solutions for the load flow using the Newton Raphson Method. In this example, we will take a polynomial function of degree 3 and will find its root using the Newton Raphson method.įor our first example, we will input the following values:ĭecimalPlaces = input ('Enter the required decimal places in the output:') ĪllowedError = input ('Enter the error allowed:') Ī (1) = input ('Enter the initial guess value:') įprintf('Required Root for the input function is : %f \n', Z) įprintf('Number of Iterations : %d\n',i) Īs we can see in the output, we have obtained the root of our input function as 1.3247. Newton Raphson Method is an iterative technique for solving a set of various nonlinear equations with an equal number of unknowns. Below are the examples mentioned: Example #1


 0 kommentar(er)
0 kommentar(er)
